DayOftheNewDan.com
Hawk Dove Game Theory
January 25, 2010
The initial goal of this was to model the most basic hawk dove game, but it then turned into an exercise in artificial life and population dynamics. The original simulation was modeled after Hingston and Barone’s Hawk Dove Model, which can be reviewed in detail in their paper Hawks, Doves and Lifetime Reproductive Fitness (www.wfg.csse.uwa.edu.au/publications/WFG2004e.pdf). The basic idea is that there is a population of hawks and doves competing for food. When two birds want the same piece of food they have two options: bluff or fight for food. If a bird bluffs he uses up a certain amount of energy to look big and mean, but will not get injured because he’ll run away without food if things get too rough. If a bird fights and loses, he is injured, which imposes a greater energy loss. When two birds meet there can be 3 possibilities:
- Hawk vs. Hawk: both fight until one is injured (selected randomly from the two hawks). Winning hawk gets 50 energy points, losing hawk is injured, relinquishing 50 energy points.
- Hawk vs. Dove: dove bluffs and hawk fights. Because the dove bluffs it never gets the food, but only relinquishes 10 energy points for the bluff. The hawk always wins, receiving 50 energy points.
- Dove vs. Dove: both bluff, a random winner is chosen. Winning dove receives 50 energy points for getting the food, losing dove relinquishes 10 energy points for bluffing.
The simulation proceeds through many rounds of simulated population interaction, with each round performing the following psuedo-code.
Remove expired food
Add new food
For each agent:
If the agent has not yet competed for food in this time period:
If food is available:
If another agent wants food:
Compete for food and update agent's nergy
Else:
Take food and update agent's energy
Subtract base energy used each turn from agent's energy
If agent's energy < deathThreshold:
Remove agent from population
If agent's energy > reproductionThreshold:
Create offspring with energy/2 and reduce agent’s energy to energy/2
The following parameters were used in the simulation:
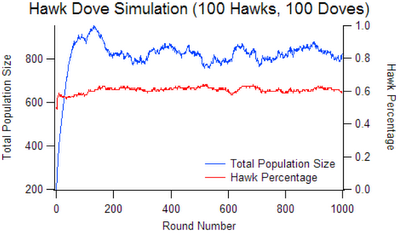
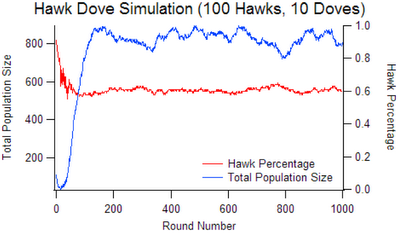
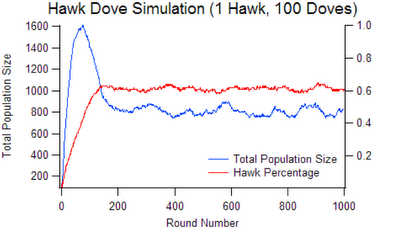
- Initial population: 100 Hawks 10 Doves, 1 Hawk 100 Doves, and 100 Hawks 100 Doves
- Energy value of food v = 50
- Energy loss for injury I = 100
- Energy loss for bluffing b = 10
- Death threshold: deathThreshold = 20
- Reproduction threshold: reproductionThreshold = 140
- Initial energy given to agents: random between d and r
- Base energy subtracted each round: 2
- Time before food expires if not eaten: 5
- Food Supply: 100 new food items per round.
After writing a simulation, which follows the rules outlined above, I came to these results: An all Dove population stabilizes near 1,790, this is the maximum population size that the environment can support. An all Hawk population will drive itself extinct. A mixed population of fewer than around 10 doves will also be driven to extinction as the hawks take over. As you can see neither hawk nor dove is an evolutionarily stable strategy (ESS), they will both be infiltrated by a small population of the other. An ESS occurs when the population consists of approximately 60% Hawks.
What is incredibly interesting about this is that nature will not necessarily find the best outcome for each species. Many more birds are allowed to live if no hawks exist. One might want to generalize this concept and apply it to human “criminals” and “goody two shoes”. It appears that there would have to be a stable percentage of criminals in the world because neither populations of all criminals or all goody two shoes are stable strategies, each would be infiltrated by a small amount of the other. So, does that mean criminals necessary?